 | singsurf.org - Geometry and the imagination |
 | singsurf.org - Geometry and the imagination |
R. Morris and M Connor
The idea is to examine one of the classic paradoxes in Greek philosophy, the Sorites or Heap paradox, and apply ideas from modern mathematics to it, in particular ideas from singularity theory/catastrophe theory and the hysteresis effect.
The basic idea behind the Sorites paradox is related to how we can interpret a continuously changing phenomena using discreet language. The classical paradox concerns a pile of sand to which grains of sand are added one at a time and the question is at what point do we classify the pile as being “a heap”? Several obvious approaches, such as saying “its a heap if it has more than a thousand grains of sand” are workable but flawed (can you with all confidence point to a pile with 999 grain and one with 1001 grains and say they are different). Hence its status as a paradox.
This question has educational implications in particular for the marking of exams and awarding of grades. In the traditional system there will be certain point distinguishing a B grade from a C grade (55%). So even though there is a small change in quality of work there will be a large difference in outcome.
The approach we have taken is to use ideas from catastrophe theory which describes how rapid states of change can arise from continuously varying phenomena. The classic example here is the stability of boats. For the most part a boat is relatively stable, small changes due to wind and tide do not greatly affect its position. However, it is possible for a sufficient large wave to take the boat away from a stable state into another (i.e. it sinks). This is observed in some of the tragic ferry accidents, once water has got through the bulkheads the boat will begin to tilt allowing more water to be taken on board. This then causes a positive feedback situation with the boat tacking on more and more water until it arrives at another stable state (at the bottom of the ocean).
The application to the Sorites is that there are two stable states: it definitely is a heap, it definitely is not a heap, and an region of instability between the two where you are unsure about its classification. Its possible to construct a mathematical model to describe this behavior using a two dimensional graph, with the number of grains of sand along the x-axis and the two stable states as points on the y-axis. With this model you can draw pictures of how an observers interpretation changes as the state of the pile changes (i.e. As grains are added and removed).
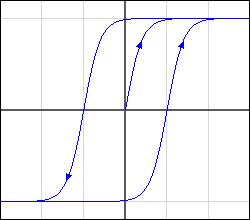
A diagram of a hysteresis loop. The x-axis can be though of as the number of grains of sand and the y-axis as the observer's interpretation, with “is a heap” at the top and “is not a heap” at the bottom.
Hysteresis mean a characteristic property that is history-dependent and shows some time lag or delay. Hence it is not just the current state which affects the outcome but also the path taken to get to that state. If a hysteresis affect is applied to the Sorites then depending on past history an observer might characterize a pile as either bing a heap or not a heap.
If we accept a hysteresis approach to Sorites then there are philosophical questions around issues of naming, classification and subjectivity. It open the way allow two interpretations of a situation which may actually conflict with each other. These two interpretations depend not on the state itself (indeed two observes may agree completely on the current state) but on the past histories which lead to this state.
In and educational context this can be applied to issues like the marking of an essay. The mark awarded might not depend solely on the quality of the essay but also on the past history between the student and the teacher.
Diana Raffman Mon May 29 2023
You are plagiarizing Raffman 2014, Unruly Words: A Study of Vague Language (Oxford U P) and also 1994 "Vagueness Without Paradox".