Main applet window General Help JavaView Help.
A major update of the asurf program. It has now can give almost perfect results for most types of singularities. Specifically
# The following selects a specific box at the specified depth, # only the component inside that box is drawn. asurf_selx=8;asurf_sely=8;asurf_selz=8;asurf_denom=16; # This line causes the curves df/dx=0, df/dy=0, df/dz=0 to be drawn. asurf_degen=0;
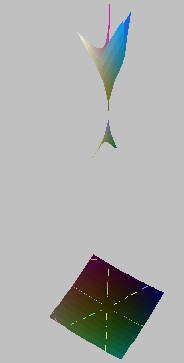
 As well as these a
bit more mathematics has been used to work out if a singularity should
lie in a box. Second derivatives are now examined in more detail. In
particular the determinant of the second derivative matrix is now
examined. The sign of this gives the diference between two lines
crossing on a face (x^2-y^2=0) or an isolated point on the face
(x^2+y^2=0) and similar fun in 3D. This has helped reduce the number of
false positive singurlarity points found.
As well as these a
bit more mathematics has been used to work out if a singularity should
lie in a box. Second derivatives are now examined in more detail. In
particular the determinant of the second derivative matrix is now
examined. The sign of this gives the diference between two lines
crossing on a face (x^2-y^2=0) or an isolated point on the face
(x^2+y^2=0) and similar fun in 3D. This has helped reduce the number of
false positive singurlarity points found.Long term stuff to do.
<definition name="Kummer surface" type="asurf"> (3-v^2) ( x^2+y^2 + z^2 - v^2)^2 - (3 v^2 - 1) p q r s = 0; p = 1 - z - x rt2; q = 1 - z + x rt2; r = 1 + z + y rt2; s = 1 + z - y rt2; rt2 = sqrt(2); <variable name="x" min="-1" max="1"> <parameter name="v" value="1.1"> <option name="course" value="8"> .... </definition>This will be the format definition will be saved in and used to communicate between client and server.
Copyright Richard Morris 2003
|
|
This work is licensed under a
Creative Commons License. (You can copy, distribute and display this works but: Attribution is required, its for Non-Commercial purposes, and it's Share Alike (GNUish/copyleft) i.e. has an identical license.) It would also be nice if you let me know (rich@singsurf.org) if you link to, redistribute, make a derived work or do anything groovy with this information. |
|
|